Ch. 10 – Basics (sines)

Figure 10.1. Illustration of basic representations and transformations of audio using a 400 Hz sine wave and complex tone consisting of 400, 600 and 1600 Hz sine waves.

Show the code 
import numpy as np
from matplotlib import pyplot as plt

Create sine waves

### Define the properties of a sine wave

frequency = 400   # Frequency
duration = 0.01   # Duration of sound
amplitude = 1.0   # Amplitude
phase = 0.75      # Phase
Fs = 22050        # Sampling rate (per second)

# This code creates the sine wave with the properties you detailed above
num_samples = int(Fs * duration) 
t = np.arange(num_samples) / Fs
x = amplitude * np.sin(2 * np.pi * (frequency * t - phase))
fig, ax = plt.subplots(figsize=(7.5, 2.75))
ax.plot(t, x, color='red')
ax.set_xlabel('Time (s)')
ax.set_title("Sine (400 Hz)")
ax.set_ylabel('Air pressure deviation')
ax.set_ylim([-1.05, 1.05])
ax.set_yticks(np.arange(-1, 1.5, 1.0)) 
ax.set_xlim([0.0, 0.01])
ax.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax.grid()
ax.annotate('', xy=(0.0025, 0), xytext=(0.0025, 1), 
            arrowprops=dict(arrowstyle='<->', mutation_scale=15, 
            color='0.3'), size=2)
ax.text(0.0025, 0.5, "Amplitude", size=12, 
        color='0.3', ha="center", va="center")
ax.annotate('', xy=(0, 1), xytext=(0.0025, 1), 
            arrowprops=dict(arrowstyle='<->', mutation_scale=19, 
            color='0.3'), size=2)
ax.text(0.00125, 0.85, "Period", size=12, 
        color='0.3', ha="center", va="center")

plt.show()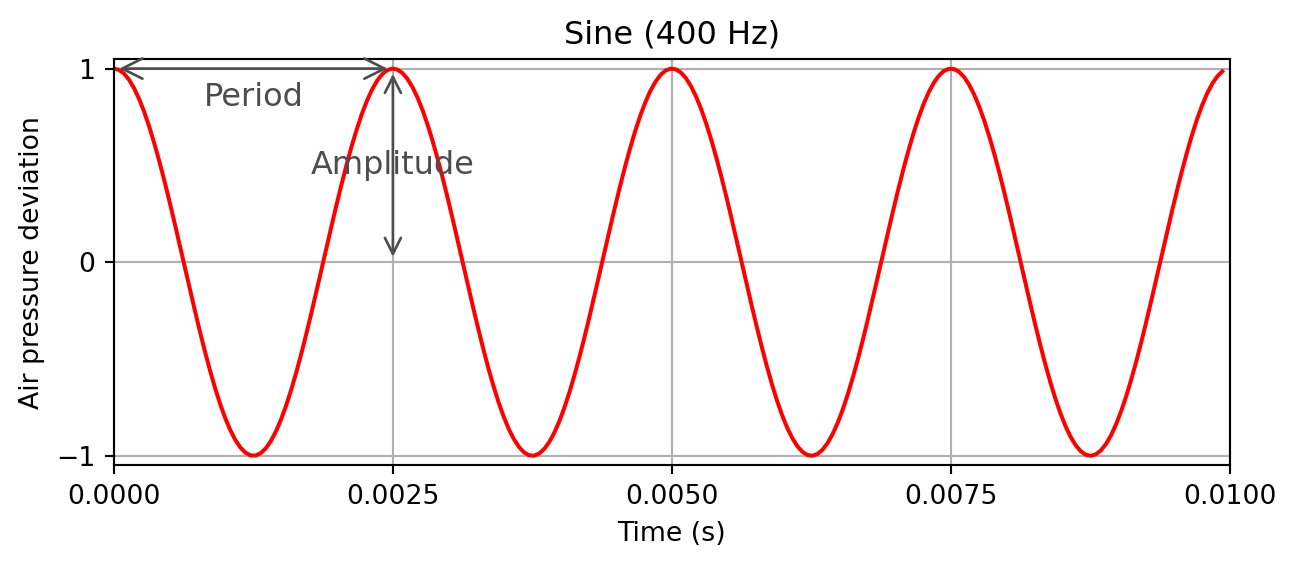

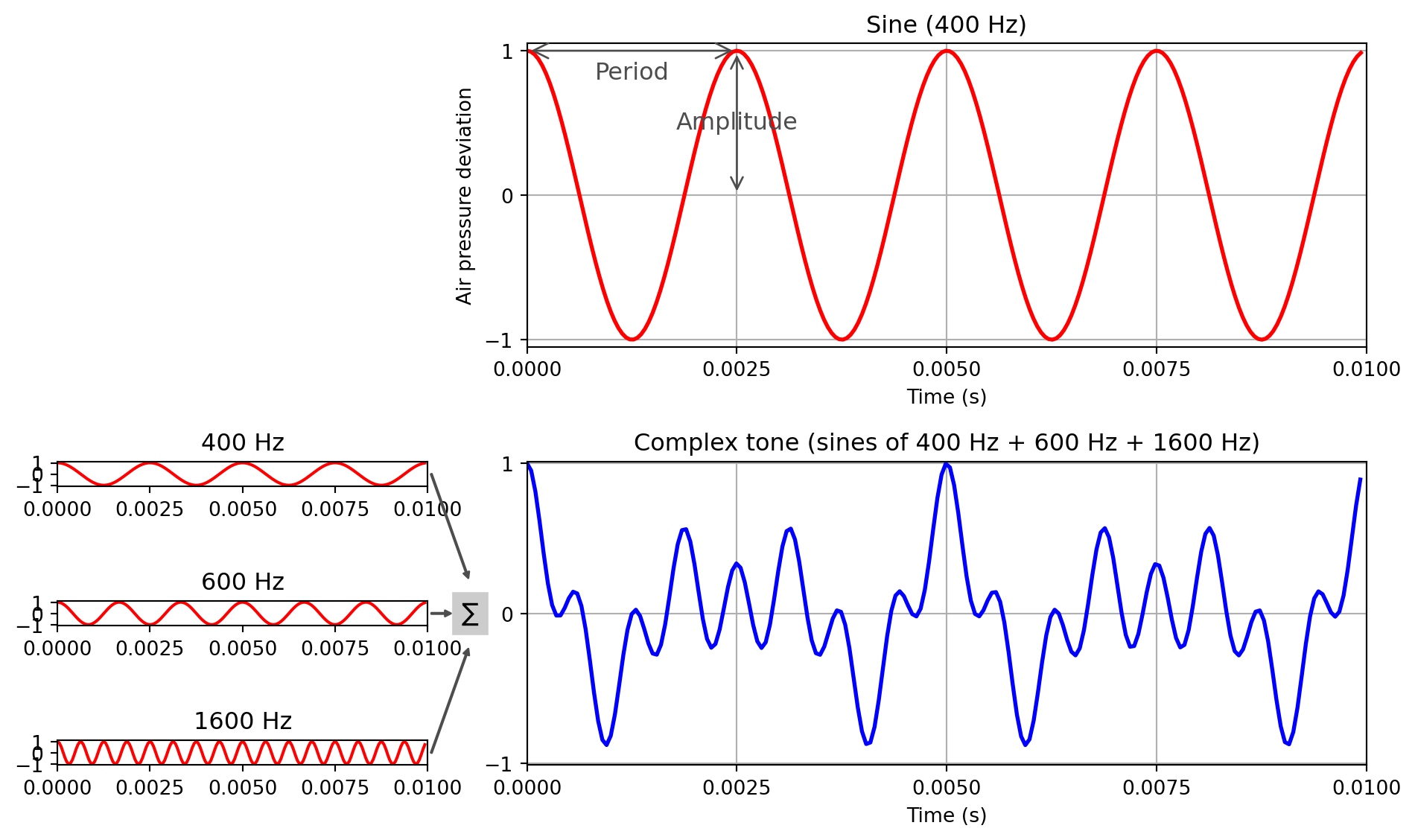
Complex sounds

Let’s combine sine waves of different frequency (400, 600, 1600 Hz).

Show the code 
import numpy as np
from matplotlib import pyplot as plt 

fig = plt.figure()
fig.set_figheight(6)
fig.set_figwidth(10)

ax1 = plt.subplot2grid(shape=(6, 3), loc=(0, 1), colspan=2, rowspan=3)
ax3 = plt.subplot2grid(shape=(6, 3), loc=(3, 1), colspan=2, rowspan=3)
ax2 = plt.subplot2grid(shape=(6, 3), loc=(3, 0), colspan=1)
ax4 = plt.subplot2grid(shape=(6, 3), loc=(4, 0), colspan=1)
ax5 = plt.subplot2grid(shape=(6, 3), loc=(5, 0), colspan=1)

frequency = 400   # Frequency
duration = 0.01   # Duration of sound
amplitude = 1.0   # Amplitude
phase = 0.75      # Phase
Fs = 22050        # Sampling rate (per second)

num_samples = int(Fs * duration) 
t = np.arange(num_samples) / Fs
x = amplitude * np.sin(2 * np.pi * (frequency * t - phase))

ax1.plot(t, x, color='red', linewidth=2.0, linestyle='-')
ax1.set_xlabel('Time (s)')
ax1.set_title("Sine (400 Hz)")
ax1.set_ylabel('Air pressure deviation')
ax1.set_ylim([-1.05, 1.05])
ax1.set_yticks(np.arange(-1, 1.5, 1.0)) 
ax1.set_xlim([0.0, 0.01])
ax1.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax1.grid()

ax1.annotate('', xy=(0.0025, 0), xytext=(0.0025, 1), 
             arrowprops=dict(arrowstyle='<->', 
             mutation_scale=15, color='0.3'), size=2)
ax1.text(0.0025, 0.5, "Amplitude", size=12, color='0.3', 
         ha="center", va="center")
ax1.annotate('', xy=(0, 1), xytext=(0.0025, 1), 
             arrowprops=dict(arrowstyle='<->', mutation_scale=19, 
             color='0.3'), size=2)
ax1.text(0.00125, 0.85, "Period", size=12, 
         color='0.3', ha="center", va="center")

# Combine several sine waves (here are three frequencies)
frequency1 = 400  
frequency2 = 600
frequency3 = 1600
duration = 0.01
amplitude = 1.0
phase = 0.75
Fs = 20050

num_samples = int(Fs * duration)
t = np.arange(num_samples) / Fs
x1 = amplitude * np.sin(2 * np.pi * (frequency1 * t - phase))  # 1st sine
x2 = amplitude * np.sin(2 * np.pi * (frequency2 * t - phase))  # 2nd sine
x3 = amplitude * np.sin(2 * np.pi * (frequency3 * t - phase))  # 3rd sine

ax2.plot(t, x1, color='red')
ax4.plot(t, x2, color='red')
ax5.plot(t, x3, color='red')

ax2.set_title("400 Hz")
ax4.set_title("600 Hz")
ax5.set_title("1600 Hz")

ax2.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax2.set_xlim([0.0, 0.01])
ax2.set_yticks(np.arange(-1, 1.5, 1.0)) 

ax4.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax4.set_xlim([0.0, 0.01])
ax4.set_yticks(np.arange(-1, 1.5, 1.0)) 

ax5.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax5.set_xlim([0.0, 0.01])
ax5.set_yticks(np.arange(-1, 1.5, 1.0)) 

fig.subplots_adjust(hspace=.001, wspace=0.5)

# Combine all three (sum and divide by 3 to keep the amplitude as original)
x123 = (x1+x2+x3)/3

ax3.plot(t, x123, color='blue', linewidth=2.0, linestyle='-')
ax3.set_xlabel('Time (s)')
ax3.set_title("Complex tone (sines of 400 Hz + 600 Hz + 1600 Hz)")
ax3.set_ylabel('')
ax3.set_ylim([-1.01, 1.01])
ax3.set_xlim([0, 0.01])
ax3.set_xticks(np.arange(0, 0.0125, 0.0025)) 
ax3.set_yticks(np.arange(-1, 1.5, 1.0)) 
ax3.grid()
fig.tight_layout()


ax2.annotate('', xy=(1.11/100, -9.3), xytext=(1.01/100, 0), 
             arrowprops=dict(width=0.5, headlength=3, headwidth=3, 
             color='0.3'), size=2, annotation_clip=False)
ax4.annotate('', xy=(1.063/100, 0), xytext=(1.01/100, 0), 
             arrowprops=dict(width=0.5, headlength=3, headwidth=3, 
             color='0.3'), size=2, annotation_clip=False)
ax5.annotate('', xy=(1.11/100, 9.3), xytext=(1.01/100, 0),
             arrowprops=dict(width=0.5, headlength=3, headwidth=3, 
             color='0.3'), size=2, annotation_clip=False)
ax4.text(1.09/100, -0.6, r'$\sum$', size=9, backgroundcolor='0.8')

plt.show()

Back to top